从TRPO到PPO（理论分析与数学证明）

背景

马尔可夫决策过程由$(S, A, P, r, \rho_0, \gamma)$六个元素构成。其中$S$是一个有限的状态空间集合，$A$是一个有限的动作空间集合。$P: S \times A \times S \rightarrow \mathbb{R}$ 表示状态转移概率函数，例如$P(s'|s,a)=0.6$表示的含义就是在状态$s$处执行动作$a$到达的状态为$s'$的概率为0.6。$r: S\rightarrow \mathbb{R}$是奖励函数，$\rho_0: S\rightarrow\mathbb{R}$是初始状态分布概率函数，$\gamma\in (0,1)$是折扣因子。

让$\pi$表示一个随机策略函数$\pi: S\times A\rightarrow [0,1]$,例如$\pi(s,a)=0.5$表示在状态$s$处选择动作$a$的概率为0.5。令$\eta(\pi)$表示基于策略$\pi$的长期期望折扣奖励：$\eta(\pi) = \mathbb{E}{s_0, a_0,\ldots}[\sum\limits{t=0}^{\infty}\gamma^t r(s_t)]$, 其中$s_0\sim \rho_0(s_0), a_t\sim \pi(a_t|s_t), s{t+1}\sim P(s{t+1}|s_t,a_t)$。

下面给出状态价值函数、状态动作价值函数、优势函数的定义：

（1）状态动作价值函数：

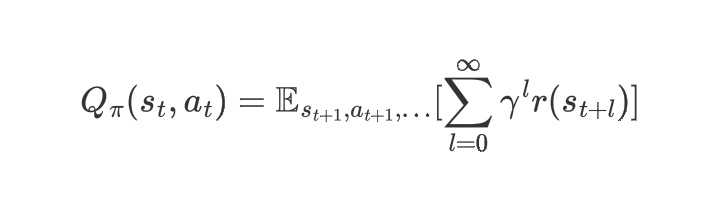
表示的是在状态$s_t$处执行动作$a_t$后获得的长期期望折扣奖励。

（2）状态价值函数:

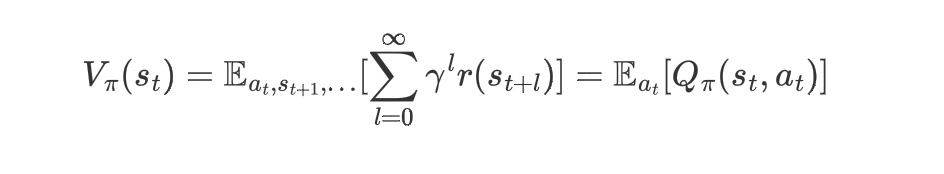
表示从状态$s_t$开始获得的长期期望折扣奖励。

（3）优势函数：

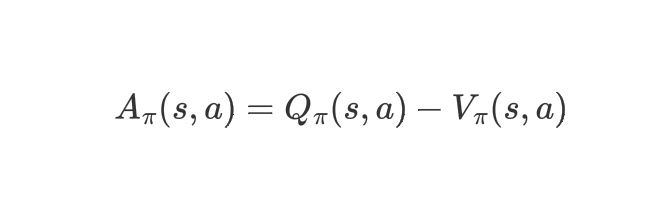
表示的是在状态$s$处，动作$a$相对于平均水平的高低。

强化学习的目标就是最大化长期期望折扣奖励 $$\eta(\pi) = \mathbb{E}{s_0, a_0,\ldots}[\sum\limits{t=0}^{\infty}\gamma^t r(s_t)]$$ 其中策略函数$\pi$可以看作是带有参数$\theta$的随机策略$\pi(s,a) = \pi\theta(s,a)$。在策略梯度算法(Policy Gradient)中，参数$\theta$的更新公式为 $$\theta{new} = \theta{old} + \alpha\nabla{\theta}\eta(\theta)$$ 这样的更新公式容易导致以下问题：如果步长$\alpha$选取不合适，那么会导致$\theta{new}$比$\theta{old}$差，当使用$\theta{new}$进行采样学习的时候，采取到的样本就是比较差的样本，再继续使用不好的样本对参数进行更新，得到的是更加不好的策略，从而导致恶性循环。TRPO算法解决的问题就是：如何选择一个合适的更新策略，或是如何选择一个合适的步长，使得更新过后的策略$\pi{\theta{new}}$一定比更新前的策略$\pi{\theta_{old}}$好呢？

1.TRPO的理论分析

1.1 不同策略的长期期望折扣奖励之间的关系

先来看一下基于策略$\pi$的长期折扣奖励 $$ \eta({\pi}) = \mathbb{E}{s_0,a_0,\ldots}[\sum\limits{t=0}^{\infty}\gamma^t r(s_t)]$$ 对于另一个策略$\tilde{\pi}$,两个策略之间的长期折扣奖励函数$\eta(\tilde{\pi})$与$\eta(\pi)$之间的关系为： $$\eta(\tilde{\pi}) = \eta(\pi) + \mathbb{E}{s_0,a_0,\ldots\sim\tilde{\pi}}[\sum\limits{t=0}^\infty \gamma^t A{\pi}(s_t,a_t)] \tag{3.1}$$ 其中$A\pi(s_t,a_t)$为优势函数，$A\pi(s_t,a_t) = Q\pi(s_t,a_t) - V_\pi(s_t)$。（证明过程见文章后面附录证明4.1）。

上述公式要注意的点是$s_0,a_0,\ldots\sim\tilde{\pi}$表示轨迹中的状态和动作都是基于策略$\tilde{\pi}$采样得到的，而$A_{\pi}(s_t,a_t)$表示的是策略$\pi$的优势函数。 为了方便公式的书写和后续求导的计算，定义 $$\rho\pi(s) = P(s_0=s) + \gamma P(s_1=s) + \gamma^2 P(s_2=s) + \ldots$$ 则公式$(3.1)$可以改写为： $$\eta({\tilde{\pi}}) = \eta({\pi}) + \sum\limits_s\rho{\tilde{\pi}}(s)\sum\limits_s\tilde{\pi}(a|s)A_\pi(s,a) \tag{3.2}$$ 证明过程见文章后面附录证明4.2。

1.2 替代函数的建立

再来回顾一下我们在背景中提出的目标：找到一个合适的步长，使得每一个更新得到的新的策略$\pi{new}$要比更新前的策略$\pi{old}$好,体现在公式上就是要求$\eta(\pi{new}) \ge \eta(\pi{old})$。

由于公式$(3.2)$中的$\rho_{\tilde{\pi}}$对$\tilde{\pi}$有强烈的依赖性，但是在更新之前我们还不知道策略$\tilde{\pi}$的具体形式，所以我们考虑找到一个$\eta(\tilde{\pi})$的替代函数：

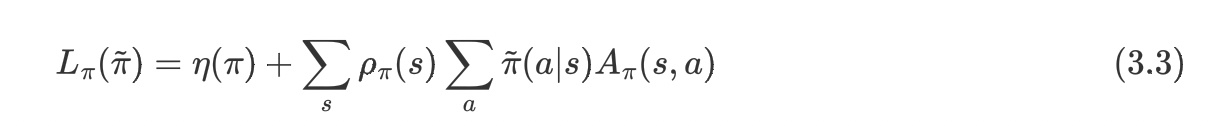
这个替代函数的作用是什么呢，可以帮助我们得到$\eta$函数的哪些性质呢？把策略$\pi$表示为带有参数$\theta$的随机策略$\pi=\pi\theta$，给出下面定理：$L{\pi{\theta_0}}(\pi\theta)$与$\eta(\pi_\theta)$在$\theta_0$处一阶近似，用公式表示为:

证明过程见文章后面附录证明4.3。

公式$(3.4)$的第二个等式可以告诉我们：在$\theta = \theta_0$附近，$\eta(\pi\theta) = L{\pi{\theta_0}}(\pi\theta)$的曲线的变化趋势相同，因为一阶导数的意义就是曲线的变化趋势。又因为这两个函数在$\theta = \theta_0$处的值相等（公式$(3.4)$的第一个等式），所以在$\theta = \theta_0$的附近，可以通过优化$L{\pi{\theta_0}}(\pi\theta)$来达到优化$\eta(\pi\theta)$的目的，注意是：$\theta = \theta_0$的附近！！！附近！！！下面给出一个一阶近似的例子：

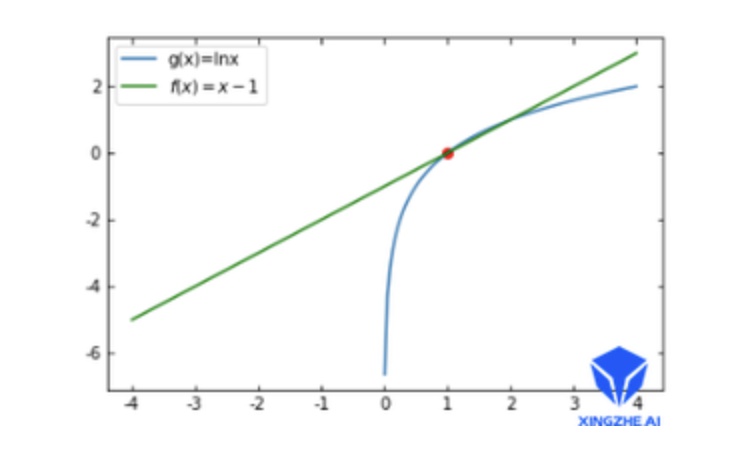
如图所示：函数$f(x) = x-1$ 与 函数$g(x) = lnx$在$x=1$处是一阶近似的，即$f(1) = g(1)$, $f'(1) = g'(1)$，所以这两个函数的曲线的变化趋势在$x=1$处是近乎相同的。

用$\pi{old}$来表示更新前的策略，定义$\pi' = argmax{\pi'}L{\pi{old}}(\pi')$ 我们采用一种软更新的方式对策略进行更新，更新公式为 $$ \pi{new} = (1-\alpha)\pi{old} + \alpha\pi' \tag{3.5}$$ 其中$\pi_{new}$就表示更新之后的策略，$\alpha$为更新步长。

部分读者在阅读到这里的时候可能会产生以下疑问：为什么不直接把$\pi'$直接当作更新之后的策略呢？$L{\pi{old}}(\pi')\ge L{\pi{old}}(\pi{old})$不是可以推导出$\eta(\pi')\ge\eta(\pi{old})$吗？

解答：因为这是一种迭代更新方式，$\pi'$只是给出了一个可以优化$\pi{old}$的方向，我们要做的是将$\pi{old}$向$\pi'$的那个方向迭代，而不是直接将$\pi'$当作更新之后的策略；另外$L{\pi{old}}(\pi')\ge L{\pi{old}}(\pi{old})$并不可以直接推导出$\eta(\pi')\ge\eta(\pi{old})$，因为$\pi'$并不一定在$\pi_{old}$的附近!

1.3 TRPO算法的推出

再来回顾一下我们最初的目的：找到一个合适的步长，使得每一个更新得到的新的策略$\pi{new}$要比更新前的策略$\pi{old}$好。那么使用软更新方式得到的策略$\pi{new}$是否比更新前的策略$\pi{old}$好呢，换句话说，是否成立$\eta(\pi{new})\ge \eta(\pi{old})$呢？其实$\pi' = argmax{\pi'}L{\pi{old}}(\pi')$给我们的优化提供了方向，我们的关键就在于如何选择合适的步长使得更新之后的策略一定是比更新之前的策略好。再思考一下，其实一定有$L{\pi{old}}(\pi{new}) \ge L{\pi{old}}(\pi{old})$, 因为$\pi{new}$是从$\pi{old}$朝着$\pi'$的方向迭代的,并且$L{\pi{old}}(\pi')\ge L{\pi{old}}(\pi{old})$。再回想一下前面我们说：在$\pi = \pi{old}$附近，$L{\pi{old}}(\pi)\ge L{\pi{old}}(\pi{old})$等价于$\eta(\pi)\ge \eta(\pi{old})$, 所以我们只需要把$\pi{new}$限制在$\pi{old}$附近即可，可以通过放在惩罚项或者约束上进行限制。如何限制两个策略的差异性呢，可以使用两个策略的KL散度：$D{KL}^max(\theta{old}, \theta{new})$，因为KL散度是用来度量两个概率分布相似度的指标。其实从这个分析我们就可以得到最终的TRPO算法了，原论文中给出了严格的数学推导，我们大概介绍一下思路(可以不看）：

设$\pi_{new}$是按照更新公式$(3.5)$得到的新策略，从论文[1]中可以得到下面不等式成立：

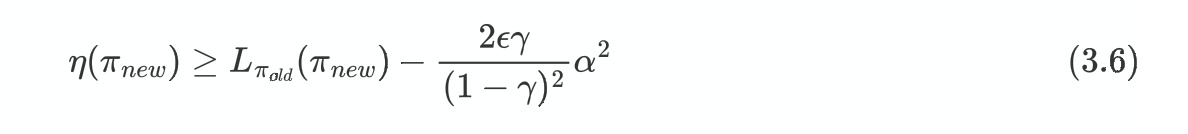
其中$\epsilon = max_s|\mathbb{E}{a\sim \pi'(a|s)}[A\pi(s,a)]|$。

我们可以令$\alpha = D^{max}{TV}(\pi{old}, \pi_{new})$, 进而成立：

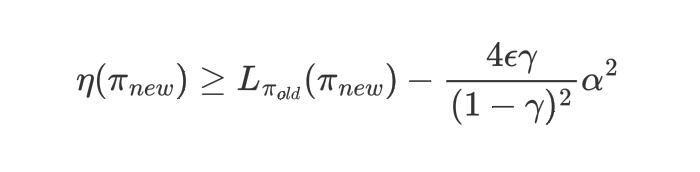
其中$\epsilon = max{s,a}|A\pi(s,a)|$。再根据不等式：$D{TV}(p||q)^2\le D{KL}(p||q)$,令$D{KL}^{max}(\pi, \tilde{\pi}) = max_s D{KL}(\pi(·|s)||\tilde{\pi}(·|s))$ 成立：

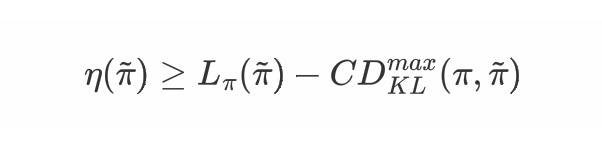
其中$C = \frac{4\epsilon\gamma}{(1-\gamma)^2}$。

给出下面策略更新算法：

假设我们根据上面这个算法得出一个策略序列$\pi_0, \pi_1, \ldots$，下面证明该策略序列是越来越好的，即$\eta(\pi_0)\le\eta(\pi_1)\le\ldots$。

令$M_i(\pi) = L{\pi_i}(\pi) - CD{KL}^{max}(\pi_i, \pi)$, 则成立：

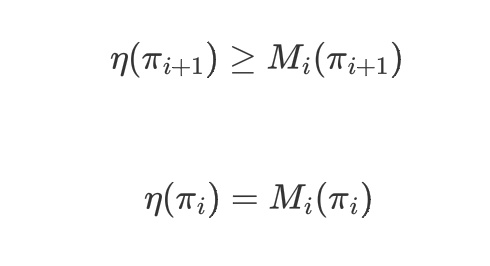
等式成立是因为当$\tilde{\pi} = \pi$时，$D_{KL}^{max}(\pi, \tilde{\pi}) = 0$。

所以成立：$\eta(\pi{i+1}) - \eta(\pi_i) \ge M_i(\pi{i+1}) - M(\pi_i)$

所以在第i次迭代时,$M_i(\pi)$可以作为$\eta(\pi)$的替代函数，从而得到的策略序列是越来越好的。进而每一个更新过后的策略$\pi{new}$都好于更新前的策略$\pi{old}$。目的达到。 如果这个数学证明没看懂没有关系，可以直接通过之前的语言分析理解TRPO算法。

为了方便将$\pi{\theta{old}}$写作$\theta{old}$, 在接下来的分析中，我们都考虑带有参数$\theta$的策略$\pi\theta(a|s)$。通过之前的分析，从而我们可以通过优化下面的式子来达到优化$\eta(\pi)$的目的：

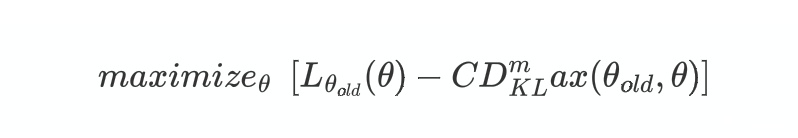
但是有C作为惩罚系数，会导致每次的$D{KL}^max(\theta{old},\theta)$的值特别小，从而导致更新的步子很小，降低更新速度，所以我们考虑将惩罚项变为约束项:

用语言理解就是在以$\theta_0$为球（圆）心，以$\delta$为半径的区域中搜索可以提高$L{\pi{old}}(\pi)$（等价于提高$\eta(\pi)$）的策略$\pi$。这就是TRPO算法。

注意到$L{\theta{old}}(\theta) = \eta(\theta{old}) + \sum\limits_s\rho{\theta{old}}(s)\sum\limits_a\pi\theta(a|s)A{\theta{old}}(s,a)$, 其中$\eta(\theta_{old})$相对于$\theta$来说是常数，可以去掉，因此公式$(3.6)$变为

1.4 重要度采样

在最开始推导公式$(3.1)$的时候，我们当时说了等号右边的$s,a$是基于策略$\tilde{\pi}$采样的，但是在真实世界中，因为在更新前$\tilde{\pi}$是未知的，所以我们没法基于$\tilde{\pi}$采样，所以我们考虑使用重要度采样，假设我们使用策略$q(a|s)$进行采样，那么我们的优化函数要有所变化：

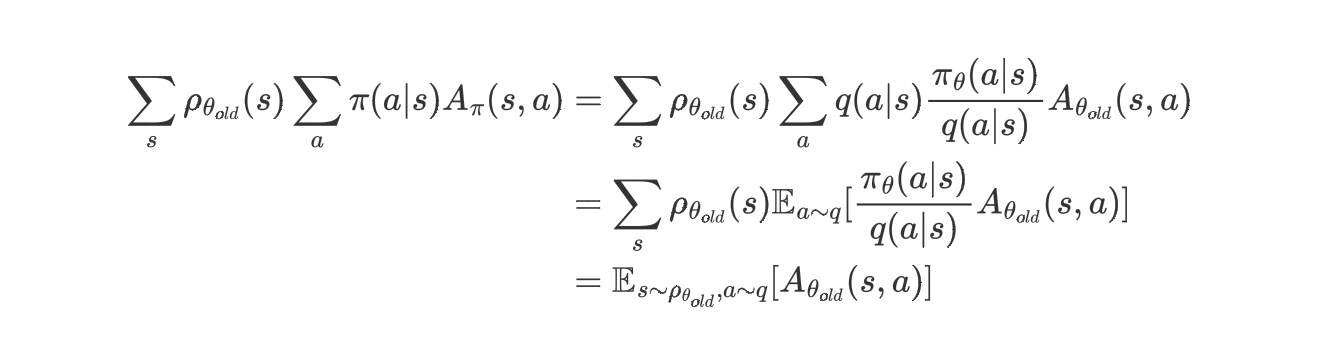
所以最终TRPO的更新算法变为：

注意：这里的$s$还是服从$\rho{\theta{old}}$的概率，即$\rho{\theta{old}}(s)$中的动作$a$的概率还是基于策略$\theta{old}$！！这里是大家比较容易理解错误的地方，误以为$s$公式中的$a$是基于采样策略$q$的。并且这里的采样概率$q(a|s)$可以是任意的，只用来采样而已！！后来TRPO算法在做的时候直接将$\pi{\theta_{old}}(a|s)$当作采样策略$q(a|S)$。

2. PPO算法的理论分析

2.1 TRPO算法的局限性

但是采样策略$q$真的可以任意吗？太任意会出现什么问题呢？我们来看下面这个例子：

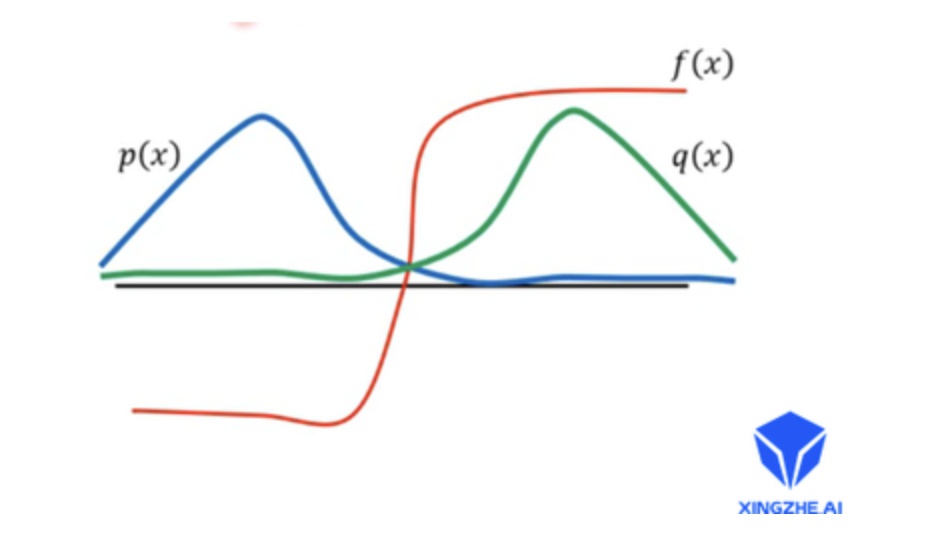
如图所示，$p(x)$是真实的分布概率，$q(x)$是采样时候使用的概率，显然二者的差异很大。设曲线$p(x),q(x),f(x)$交点的横坐标为$x=0$，所以在采样的时候，我们大多采到的是$x>0$的点，因为$q(x)$在正半轴的概率值更大，所以我们最终得到的$\mathbb{E}x[f(x)]$的值为正值，但是真实的状况是，$x$大多分布在负半轴，真实的$\mathbb{E}x[f(x)]$应该为负值，这就是由于采样概率和真实概率差距过大导致的误差。

所以我们还得限制采样策略$q(a|s)$和更新策略$\pi(a|s)$的相似度，使得他们尽可能的相像，这就是PPO算法要做的事情了。

2.2 PPO算法

第一种思路：记得我们在分析TRPO算法中，使用了KL散度限制了策略$\pi{\theta}(a|s)$和策略$\pi{\theta{old}}（a|s)$的相似度，使得他们两个的差距不能太大，所以我们考虑直接用$\pi{\theta{old}}(a|s)$当作采样策略$q(a|s)$，所以这就同时限制了采样策略和策略$\pi\theta(a|s)$的差距，一举两得，这就得到了PPO算法：

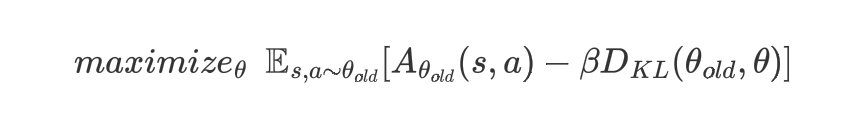
注意到这里的$\rho(s)$公式中的$a$的概率也是基于策略$\theta_{old}$的。

2.3 PPO2算法

第二种思路：在优化公式中对$q(a|s)$和$\pi_{\theta}(a|s)$进行限制，采用了截断函数，当两个函数的比值过大时，用$1+\epsilon$截断，当两个函数的比值过小时，采用$1-\epsilon$截断。PPO2算法如下：

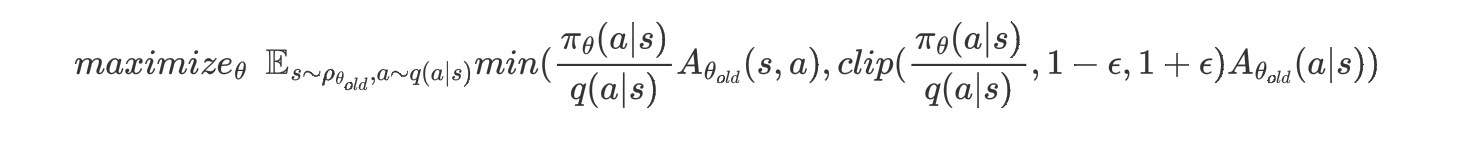
其实这里的采样策略$q(a|s)$是可以使用任意采样策略的，可能是为了效果更好，在PPO的论文中，依然按照TRPO算法的方式，将$\pi{\theta{old}}(a|s)$作为采样策略$q(a|s)$:

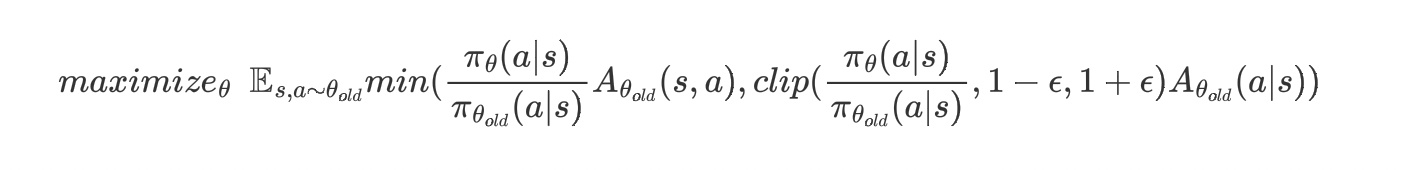
3.参考文献

[1] Kakade,Sham and Langford,John. Approximately optimal approximate reinfocement learning(https://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=EAB75A180B3AE59A7A516BF93A00863C?doi=10.1.1.7.7601&rep=rep1&type=pdf). In ICML, volume2,pp.267-247,2002.

[2] R.Sutton, D.McAllester, S.Singh, and Y.Mansour. Policy gradient methods for reinforcement learning with function approximation(https://homes.cs.washington.edu/~todorov/courses/amath579/reading/PolicyGradient.pdf). Neural Information Processing Systemsm,13,2000.

[3] J.Schulman, S.Levine, P.Moritz, M.I.Jordan, and P.Abbeel."Trust region policy optimization"(https://arxiv.org/abs/1502.05477). In: CoRR, ans/1502.05477(2015).

[4] Proximal Policy Optimization Algorithms](https://arxiv.org/abs/1707.06347), Schulman et al. 2017

4.附录证明

4.1 证明：$\eta(\tilde{\pi}) = \eta(\pi) + \mathbb{E}{s_0,a_0,\ldots\sim\tilde{\pi}}[\sum\limits^\infty\gamma^t A_\pi(s_t,a_t)]$

$$\eta(\pi) = \mathbb{E}{s_0, a_0,\ldots}[\sum\limits{t=0}^{\infty}\gamma^t r(s_t)] = \mathbb{E}[V_\pi(s_0)]$$

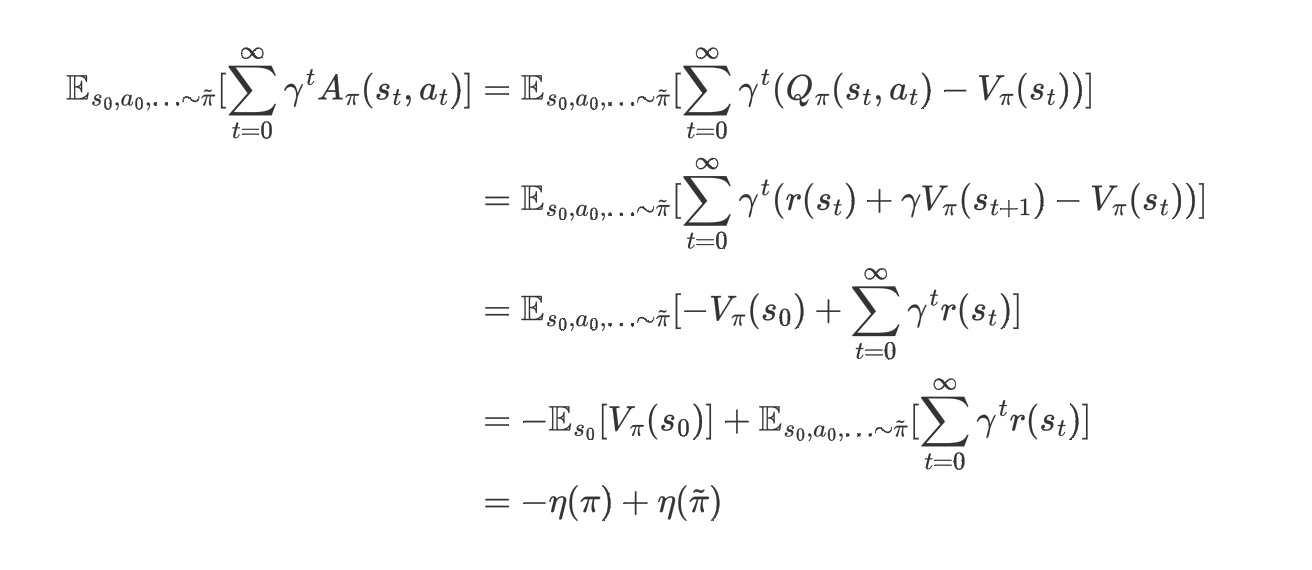
4.2 证明：$\eta(\tilde{\pi}) =\eta(\pi) + \sum\limits_s\rho{\tilde{\pi}}(s)\sum\limits_a\tilde{\pi}(a|s)A{\pi}(s,a)$

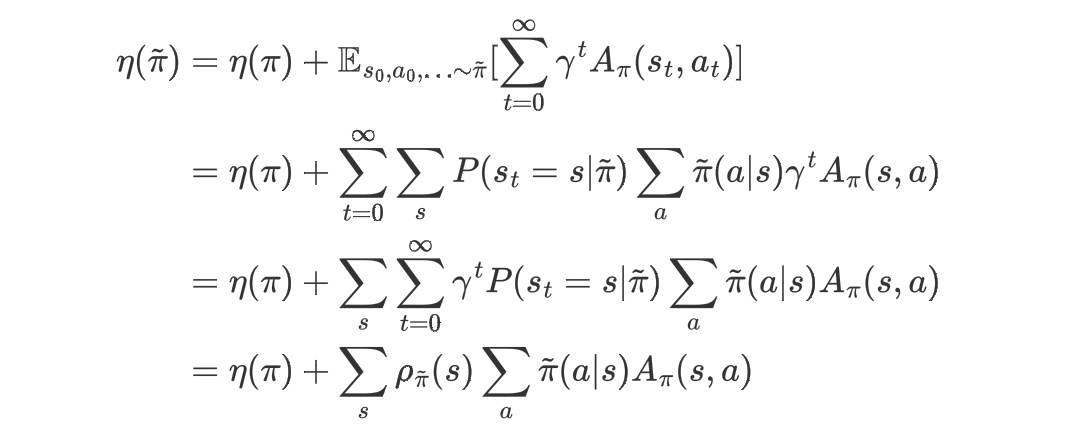
4.3 证明：

$$L\pi(\tilde{\pi}) = \eta(\pi) + \sum\limits_s\rho\pi(s)\sum\limits_a\tilde{\pi}(a|s)A\pi(s,a)$$当$\tilde{\pi} = \pi$时：$$L\pi(\pi) = \eta(\pi) + \sum\limits_s\rho\pi(s)\sum\limits_a\tilde{\pi}(a|s)A\pi(s,a)$$对于每一个$s$有

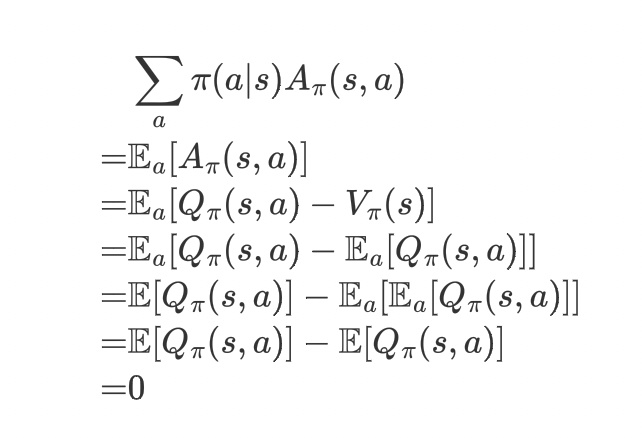
上述推导过程中第五行到第六行的推导过程中的$\mathbb{E}a[\mathbb{E}a[Q\pi(s,a)]]$ = $\mathbb{E}a[Q\pi(s,a)]$ 是因为期望的期望等于期望,从另一个角度来看这个等式，$\mathbb{E}a[Q_\pi(s,a)]$的结果与a无关，相当于一个常数，所以再对a求期望的话，相当于对常数求期望，等于常数本身。

再证明公式$(3.4)$的第二个等式：$\nabla{\theta}L{\pi{\theta_0}}(\pi\theta)|{\theta=\theta_0} = \nabla\theta\eta(\pi\theta)|{\theta=\theta_0}$

我们有:$$L{\pi{\theta_0}}(\pi\theta) = \eta(\pi{\theta_0}) + \sum\limits_s\rho{\pi{\theta_0}}(s)\sum\limits_a\pi\theta(a|s)A{\pi{\theta_0}}(s,a)$$ 两边对$\theta$求导（注意任何和$\theta_0$有关的式子在对$\theta$求导的时候都视为常数）得: $$\nabla\theta L{\pi{\theta_0}}(\pi\theta) = \sum\limits_s\rho{\pi{\theta_0}}(s)\sum\limits_a\nabla\theta\pi\theta(a|s)A{\pi{\theta_0}}(s,a)$$ 进而成立： $$\nabla\theta L{\pi{\theta_0}}(\pi\theta)|\theta = \theta_0 = \sum\limits_s\rho{\pi{\theta_0}}(s)\sum\limits_a\nabla\theta\pi\theta(a|s)|{\theta = \theta_0}A{\pi{\theta_0}}(s,a)$$

由论文[2]可知： $$\nabla\theta\eta(\pi\theta) = \sum\limits_s\rho{\pi\theta}(s)\sum\limits_a\nabla\theta\pi\theta(a|s)Q{\pi\theta}(s,a)$$

又因为

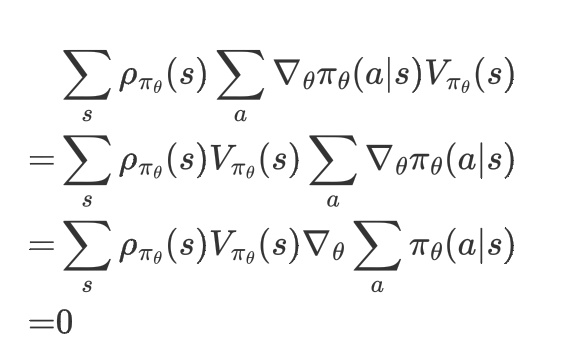
上述推导过程中第一行到第二行是因为$V{\pi\theta}(s)$与$a$无关，所以可以提到$\sum\limits_a$的前面。第二个式子到第三个式子是因为求和的导数等于导数的求和。第三个式子到第四个式子是因为对于每个$s$来说都成立：$\sum\limits_a\pi\theta(a|s)=1$,然后1对$\theta$求导等于0，即$\nabla\theta\sum\limits_a\pi\theta(a|s) = \nabla\theta1 = 0$。

所以可得：

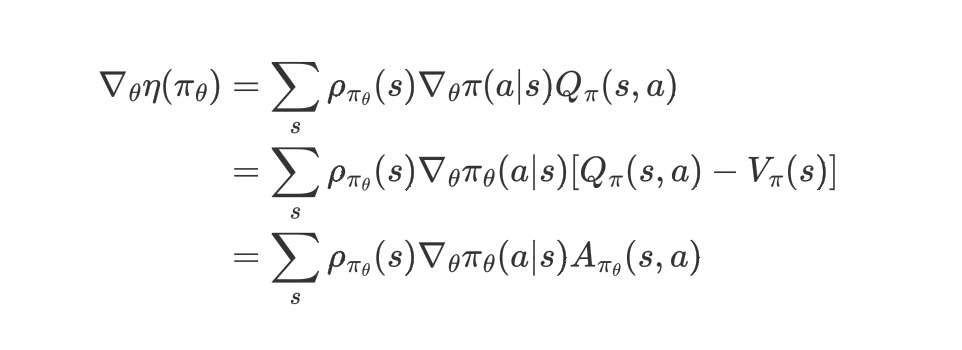
进而成立：

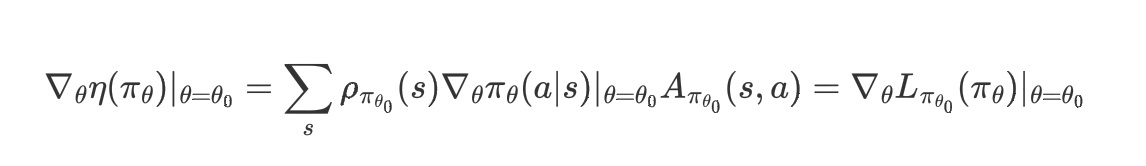
命题得证。